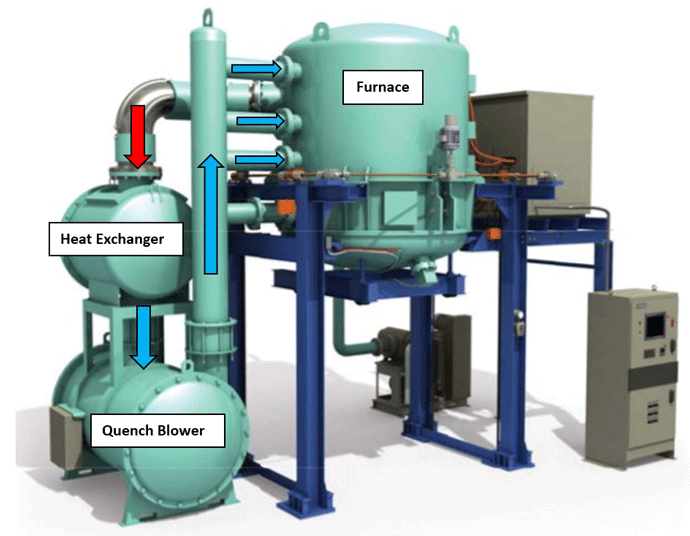
In this article, we focus on heat exchangers used in vacuum gas quenching furnace systems (Fig. 1) and examining their design and function. We will also be reviewing the similarities and differences between internal and external types of heat exchangers as well as the advantages and limitations of each design.

In vacuum processing, the load being heated in the furnace is rapidly cooled at the end of the heat cycle to impart desired physical properties in a process referred to as quenching. Although the metallurgical reasons for quenching vary depending on the process used, in all cases the goal is to quickly cool the load. Gas quenching involves introducing an inert gas (i.e. nitrogen, argon, or helium) into the furnace and rapidly circulating it through the heating chamber under pressure to remove the stored thermal energy from the load. While being circulated, the gas is forced through a heat exchanger to remove its heat.
There are several interesting and important factors that play a role in the design of a heat exchanger used for quenching and cooling of workloads in a vacuum furnace. In order to understand the function of the heat exchanger in the quenching process, we first want to review the fundamentals of the heat exchanger operation.
A heat exchanger is a device that transfers heat from one fluid (liquid or gas) to another fluid (liquid or gas) without the two fluids coming in direct contact. The type of heat exchanger typically used in a vacuum furnace is the finned tube type. Heat is first transferred from the hot gas to the fins and then to the tubes by convection, then through the tube wall by conduction and finally from the tube interior to the cold fluid inside the tube, again by convection. The efficiency of a heat exchanger is highly dependent on the mode of heat transfer, with convection being the dominant form of heat transfer in fluids. However, the conductivity of the materials must also be considered.
The basic equation (Equation 1) governing convection heat transfer is Newton’s law of cooling.
(1) Q = hA(Ta – Tb)
Where:
- Q is the heat transferred [W]
- h is the overall heat transfer coefficient [W/m2K]
- A is the surface area through which the heat is being transferred [m2]
- Ta is the temperature of the solid material (i.e. the tubes) releasing its heat [K]
- Tb is the temperature of the fluid (i.e. water or air) [K]
The above equation tells us that in order to design a heat exchanger for maximum heat transfer, the heat transfer coefficient (h) and surface area (A) must be maximized, since the temperatures, Ta and Tb are process variables and independent of the heat exchanger design.
With respect to the heat transfer coefficient (h), we find it is dependent on several factors:
(a) The properties of the fluid (viscosity, density, conductivity, etc.)
(b) The velocity of the fluid flow
(c) The (turbulent or laminar) nature of the flow
(d) The conductivity of the solid material transferring the heat (the tubes and fins in a finned tube heat exchanger)
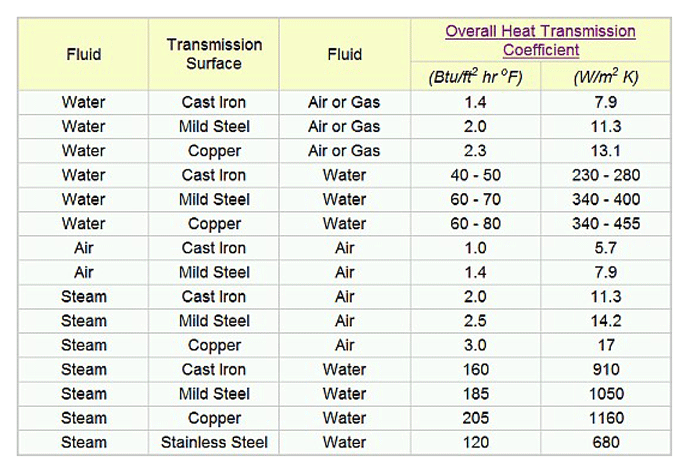
Since the calculations involved in determining the heat transfer coefficient are complex, physical testing is often used to gain an empirical understanding of this critical value as well as the ability to successfully quench a part. The heat transfer coefficient (Table 1) can also vary by an order of magnitude depending on many variables, especially when a phase change occurs, such as water boiling into steam.
In order to maximize the heat exchanger performance, we must consider the thermal conductivity of the material in which the tubes and fins are made from. Thermal conductivity is a property that quantifies the amount of heat a material will transfer (conduct) when exposed to a given temperature difference across its length or width and is the inverse of the resistivity, or “R-value”.
Heat transfer by conduction from one material to another occurs at the molecular level. Heat energy is kinetic in nature since the molecules of all materials vibrate with an energy proportional to the absolute temperature of that material. As such, when hotter (faster vibrating) molecules come into contact with cooler ones, they transfer their kinetic energy through physical collisions thus increasing the temperature of the cooler molecules.
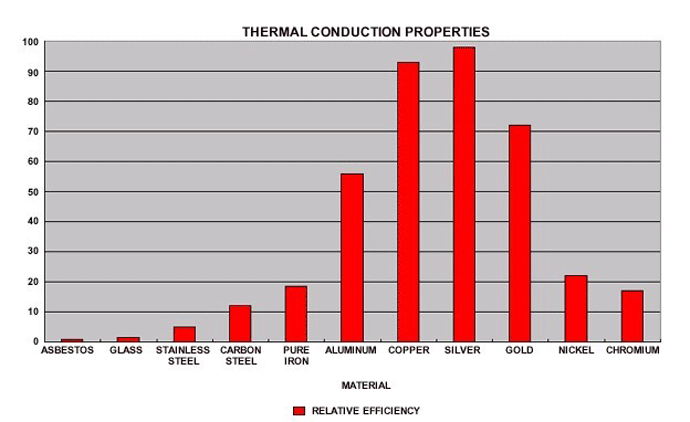
The thermal conductivity of various common materials (Fig. 2) tells us that a heat exchanger should be made from either silver, gold, copper, or aluminum. As a practical cost matter, less-expensive metals like copper and aluminum are commonly used. It is also important to note the significant conductivity difference between stainless steel and copper. Copper is 18 times more conductive than stainless. In applications where copper does not have the requisite mechanical strength and/or oxidation resistance, stainless steel is used. In some cases, a combination design is used with stainless steel tubes and copper or aluminum fins. In those instances where pressure and temperature are less severe, the tubes themselves can be made of copper and the fins of either copper or aluminum (Fig. 3).

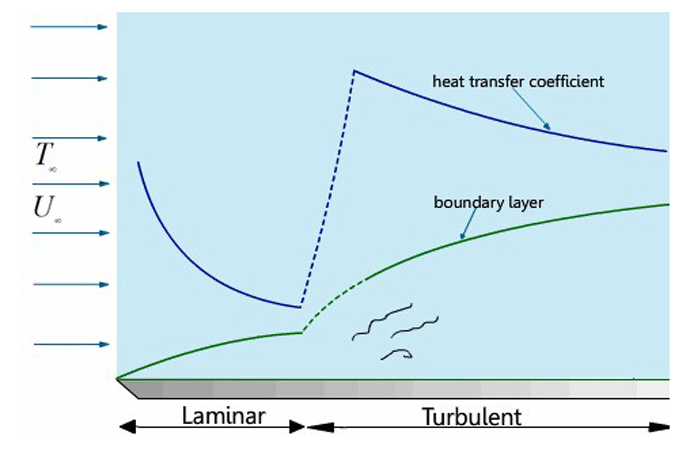
The next factor to consider is the nature of the fluid flow – laminar or turbulent. The velocity of the fluid at the surface of the heat exchanger tubes or fins is considered to be zero. This is referred to as the “no-slip” condition (Fig. 4).
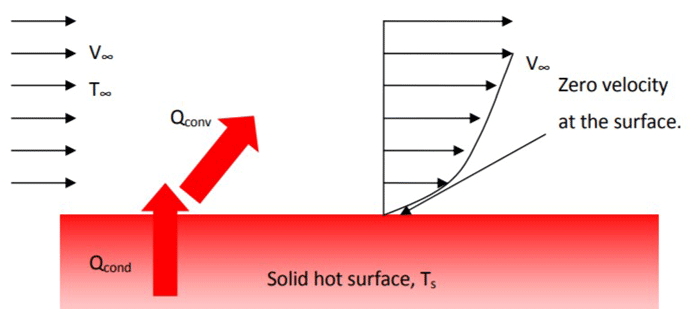
The heat transfer from the material to the fluid layer immediately at the surface involves only conduction, since at the microscopic level the fluid is motionless. This fact makes the thermal conductivity of the solid material of paramount importance for the transferring of heat. One of the objectives in heat exchanger design is to minimize the thickness of this no-slip layer since it impedes the heat transfer of the fluid. This is done by incorporating turbulent fluid flow into the heat exchanger design.
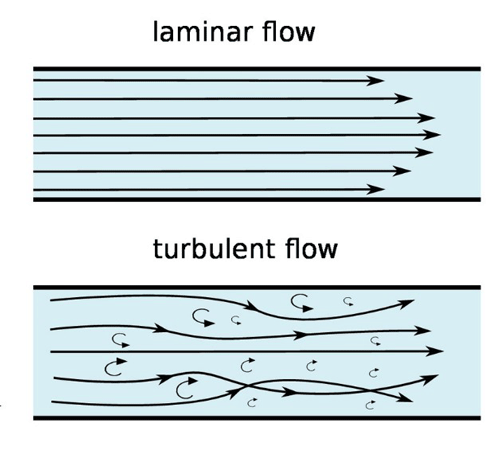
The capacity to transfer heat between the tubes and fins in a heat exchanger and the fluid (the quenching gas on the one side and the cooling water on the other) is greatly influenced by the turbulence of the flow. Laminar (non-turbulent) flow (Fig. 5) occurs when a fluid flows through a passage in separate parallel layers, with no mixing between the layers. This occurs at low velocities, where there are no cross-flows perpendicular to the direction of flow, nor swirls or eddies. In laminar flow, the motion of the particles of the fluid is very predictable and orderly. Turbulent flow is characterized by aggressive mixing of the different fluid layers and is necessary for the greatest transfer of heat energy from the surface to the fluid. Turbulent flow minimizes the thickness of the stagnant, insulating film of fluid in the no-slip region. Consequently, more heat is transferred from the tube to the fluid as convection increases (Fig. 6).
In the following section, we continue our discussion on heat exchangers by talking about the effect of surface area and other variables on their efficiency, why and how fins are used, the effect that a pressure drop has on their operation and examine the use of internal versus external heat exchangers in vacuum furnaces.
In the article above, we identified the variables most impactful of heat exchanger design and explained the significance of the convection heat transfer coefficient, the thermal conductivity of the tube material, fin material, and the importance of turbulent flow. Reviewing Newton’s law of cooling, Q = hA(Ta – Tb), another variable playing a critical role is the surface area (A) available for heat transfer. Put simply, the greater the area of heat exchange the more effective the heat exchanger will be. For this reason, one of the most important design goals for heat exchanger engineering is the maximizing of the area available for heat transfer while at the same time minimizing the physical size of the exchanger.
Heat Exchange Area
For many cases of heat exchanger design, including vacuum furnace quench systems, the heat energy must be transferred between a fluid with a high heat transfer coefficient and a fluid with a low heat transfer coefficient. This is the case for finned heat exchangers used in vacuum furnace quench systems, where the high heat transfer fluid is water and the low heat transfer fluid is air. If the area available for heat exchange were the same on both sides of the heat exchanger (which would be the case with unfinned tubes), its performance would be limited to the less effective heat transfer occurring between the hot air and the tubes. In order to make the exchanger operate efficiently, the tube surface area would need to be made prohibitively large.
The use of fins can be used to increase the heat exchange area on the airside of the exchanger which will help achieve a relative balance between the heat transfer rates on both the air and the watersides, as well as the tubes. The addition of fins to a heat exchanger increases the effective heat transfer area on the airside by 15 times (or more) in comparison to a non-finned design. However, the amount of heat transfer does not increase by the same proportion because the effectiveness of heat transfer via the fin surface area is not as great as that of the tube surface area. This is because the heat that is absorbed at the end of the fins experiences more heat flow resistance than both the base of the fins and the tube wall, resulting in diminishing returns as the fin length increases. The use of fins allows for a very compact and efficient heat exchanger design.
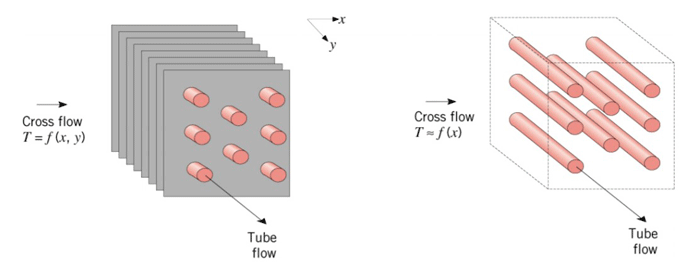
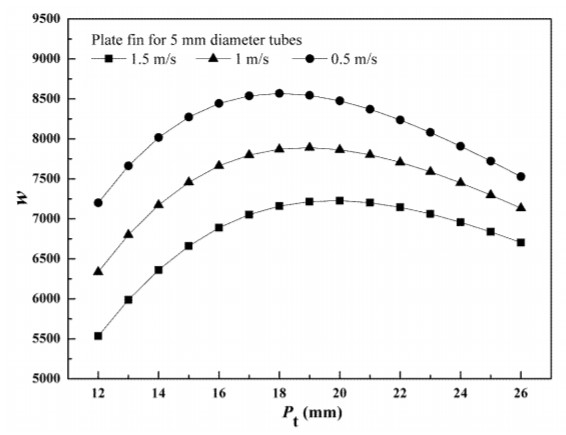
In addition to increasing the fin length, another way the fin surface area can be increased is by increasing the number of fins. Much in the same way that increasing the fin length beyond an optimum length results in no further gains in heat transfer efficiency, a similar relationship exists between the heat transfer and the number of fins utilized (Fig. 9). There is an optimum number of fins per linear meter of tube length that will offer the greatest contribution to heat transfer. Beyond this optimum number, additional fins added to the design will result in decreasing the heat transfer efficiency due to an unwanted resistance to airflow within the heat exchanger. Having more fins than necessary will also be a waste of materials.
Flow Resistance
One of the factors to consider when designing and selecting a heat exchanger is the resistance to flow, on both the airside (Fig. 10) and the waterside of the unit.
The methodologies used to optimize the heat transfer efficiency of a heat exchanger (increased fin area, turbulent fluid flow, and increased fin density) all increase the pressure drop across the exchanger and its resistance to the flow of air. This is important for several reasons. First, the fan required to push the quench air through the exchanger must be carefully sized to account for the pressure drop through the exchanger. If the pressure drop is not properly accounted for and the blower needs to be increased after the fact, it can be problematic. Due to the three laws of fan design (Fig. 11), the power required to move a given volume of air through a heat exchanger varies to the third power of the ratio of any change in airflow volume.

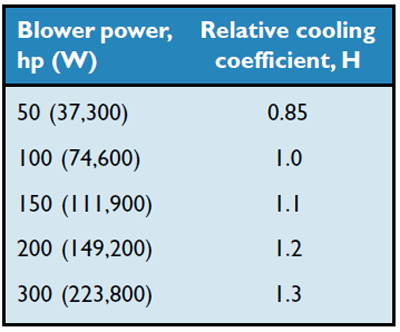
For example, if you undersize a quench system blower and later realize that you need to increase the airflow by a factor of 2, the power required to operate the fan will increase by a factor of (23), or 8 times! This would require a blower motor 8 times more powerful than the original one and quite likely a whole new blower unit. When comparing relative rates of heat transfer for variously sized quench blowers (Table 1), the fans laws are not the only impediment to increased cooling rates – the improvement in quench speed is proportionally much less than an increase in blower size. Everything else being equal, increasing the blower’s power will result in a disproportionally small improvement in the cooling rate.
Another reason the pressure drop through the heat exchanger is so critical is due to the heat generated by the friction of the air moving through the unit. A greater pressure drop results in an increase in friction and therefore in heat generated. This additional heat generated from friction must be also removed by the heat exchanger in addition to the heat being removed from the furnace load during the quenching process. Keeping this in mind, a quench fan with a 150 kW (200 HP) motor, for example, adds nearly 150 kW (500,000 BTUH) to the heat load which represents a 5°C (9°F) increase in quench air temperature for a 5 bar, 300 m3/min (10600 ft3/min) quench system. Failure to take this into consideration can result in an undersized quench cooling system.
Internal and External Heat Exchangers
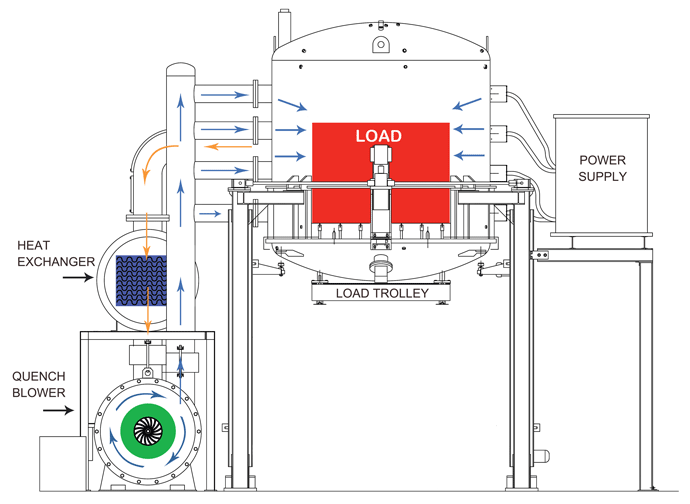
Vacuum furnaces can be designed with the blower, heat exchanger and quench piping either on the inside or the outside of the vacuum chamber, referred to as internal and external quench designs, respectively. Although these designs provide comparable performance, there are benefits and drawbacks to each.
The internal quench system offers the advantage of compactness since it occupies less floor space than the external design. This is somewhat offset out by the need to leave clearance around the furnace for maintenance access via personnel and forklift, minimizing the net gain in floor space. Another benefit of the internal design is that a separate housing for the quench blower and heat exchanger is not required. This comes at a price, however, in that the quench blower motor, driveshaft, and bearings are closer to the heat generated in the furnace hot zone, and therefore more vulnerable to heat-related failure. Furthermore, these components are more difficult to repair or replace in the internal quench design and can sometimes require the removal of the entire hot zone. Also, since the heat exchanger is inside the furnace chamber, significant damage can occur to the furnace interior if it develops a water leak.
Water Supply
An often overlooked aspect of heat exchanger design is the supply of cooling water. Flow, pressure, pressure drop, and even the quality of the water play a pivotal role in ensuring that the heat exchanger achieves its full potential and its design parameters are not compromised.
Summary
We often take heat exchanger performance for granted and it is often one of the last places we look when problems arise. We now know to ask the right questions of our OEM suppliers and question our cooling water suppliers to ensure that these systems are working at peak efficiency.
References:
- Vac-Aero International (https://vacaero.com)
- Simon Fraser University (https://www.sfu.ca)
- Artisan Distiller (http://www.artisan-distiller.net/phpBB3/index.php)
- GlassBlower (http://glassblower.info/index.html)
- Hawken Support (https://hawkensupport.com)
- Quora.com (https://www.quora.com)
- CFDSupport (https://www.cfdsupport.com/)
- Tecnico Lisboa (https://id.tecnico.ulisboa.pt/cas/login?locale=en)
- Gao, Yifeng, Ji Song, Jingdan Gao, Guoliang Ding. Fin Design For Fin-And-Tube Heat Exchanger With Microgroove Small Diameter Tubes for Air Conditioner. 2013
- Jian-FengYang, MinZeng, Qiu-WangWang. Numerical investigation on the combined single shell-pass shell-and-tube heat exchanger with two-layer continuous helical baffles. 2014
- Eldridge USA (https://eldridgeusa.com)
- EPRI Center for Materials Fabrication (https://www.epri.com/#/?lang=en)
- Vac-Aero International (https://vacaero.com)
