Abstract
For many years, ASTM E384 has stated that test forces from 1 to 1000 gf can be used to determine the Vickers or Knoop micro-indentation hardness. But, is it realistic to consider using very low test forces when the indents are measured with a light optical microscope? ASTM E92 is being resurrected and changed to cover all test loads, micro- and macro-loads, from 1 gf to 120,000 gf. Most micro-indentation hardness testers manufactured over the last 50 years or more have provided the user with a 10X objective used to find the area of interest for testing and one measurement objective, 40X magnification being the most common. A few testers have offered 50X or 60X objectives to measure the indents. It is rare to find a tester with a multiple objective (and indenter) turret, such as the DuraScan system which has ports for 2 indenters and 4 objectives. But, even with the highest quality 100X objective, indents smaller than ~15 μm in length cannot be measured with adequate precision for realistic work. The ASTM standards should eliminate recommendation of use of test loads <50 gf for Vickers and <20 gf for Knoop.
Introduction
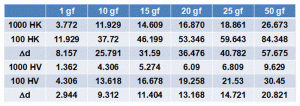
In both ASTM E384 (Micro-indentation Hardness Test Standard) and the proposed revision and re-instatement of E92 (to cover both Macro- and Micro-Loads for Vickers and Knoop), test forces below 25 gf for both Vickers and Knoop testing are listed as permissible for use. The proposed E92 lists test forces for Vickers macro-testing up to 120 kgf , although no machine built in some time has provided forces above 50 kg. The original Vickers testers made in England did use test forces up to 120 kgf, but that is a historical fact, irrelevant today.
Discussion
Why do I object to listing test forces below 25 gf? Well, the answer is right in Table 3 of the proposed E92 document. This table states that the recommended minimum diagonal length to be measured with a light microscope is 14.5 μm using a 100X objective with a 0.95 NA. However, most micro-indentation hardness testers only provide indent measurement objectives at 40X or 50X. A few systems, such as the Struers’ DuraScan systems offer an optional turret that can accommodate two indenters and four objectives of varying magnification, as shown in Figure 1. For a 40X objective, with an NA of 0.65, the minimum recommended diagonal length to measure is 21 μm. If the NA of the 40X objective is 0.55, the minimum recommended diagonal length to measure is 25 μm. If the system has a 50X objective, which is less common, and an NA of 0.65, the recommended minimum diagonal length to measure is 21 μm. In paragraph A1.4.9 of the proposed E92 test method, it states that in an indirect verification, if the diagonal length is <20 μm, indirect verifications using a certified test block is not recommended. Then, why recommend using test loads below 25 gf? Also, E384 should not recommend using test forces <25 gf. My reasoning is as follows.
 |
 |
| Figure 2: Vickers mean diagonal length versus HV for the 6 test forces. | Figure 3: Knoop long diagonal length versus HK for the 6 test forces. |
 |
 |
| Figure 4: Test force versus diagonal length for steels with 100-1000 HV or HK. | Figure 5: Difference in diagonal lengths for 100 versus 1000 HV or HK hardness numbers as a function of test force. |
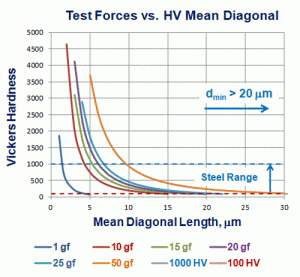
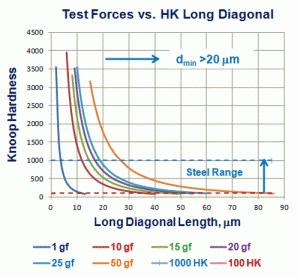
I have calculated HV and HK diagonal values for the range from 100 to 1000, typical for steels from the purest iron produced to the surface hardness of a nitrided steel using 1, 10, 15, 20, 25 and 50 gf test forces. Figure 2 shows a plot of HV versus mean diagonal length using these six test forces for the Vickers scale and Figure 3 shows similar data for the Knoop hardness scale. Note that even at a 50 gf load, only a fraction of the steel hardness range has diagonals >20 μm.
Of course, a steel specimen tested with both Knoop and Vickers indenters will not have the exact same hardness. ASTM E140 shows a 20 unit difference in HK vs. HV for steel with 68 HRC hardness and we know that HK will rise for a given specimen as the test force drops below 500 gf with the rise increasing as the test force decreases and the specimen hardness increases. HV is higher than HK at 67 and 68 HRC, while HK is greater from 20-65 HRC. At 20 HRC, there is a 13 unit difference between the Knoop and Vickers hardness. At 55 HRB, the Vickers hardness is 100 while the Knoop hardness is 112. E140 does not state a test force for Vickers. E140 states that the test forces for the Knoop conversions was 500 gf and “over” (whatever that means). So the data shown for the Knoop test using the 6 test forces does not take into account that the numbers will increase as the test force decreases for the same specimen. Nevertheless, the comparisons are acceptable.
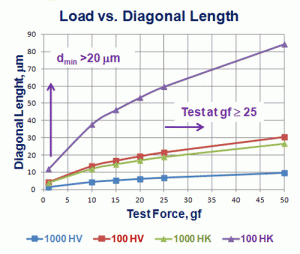
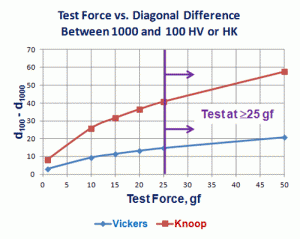
Figures 4 and 5 show plots of the six test forces used versus the mean Vickers diagonal length or the long Knoop diagonal for the 100-1000 hardness number range for steels. Again, it is obvious that the Knoop indenter has greater validity for tests with test forces ≤50 gf in this hardness range, but there is really no value in recommending use of test forces <25 gf for either test, and especially not for test forces <20 gf. Figures 4 and 5 further illustrate the better sensitivity of the Knoop compared to the Vickers test at loads ≥25 gf. For test forces above 25 gf, Knoop has a wider variation in diagonal length, and thus is better able to discriminate minor hardness differences with better precision at 25 or 50 gf test loads than the Vickers test can. Table 1 lists the hardness differences.
 |
 |
| Table 1: d100 – d1000 for Range of Steel Hardness in HV and HK. | Figure 6: Relationship between the long Knoop diagonal to the mean Vickers diagonal as a function of the equivalent HRC hardness. The mean ratio is 2.724. |
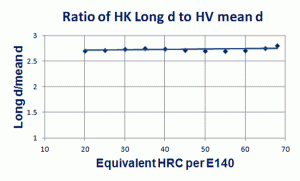
Because the Knoop long diagonal is ~2.7 times greater in length than the mean Vickers diagonal for the same test force and same hardness specimen, Figure 6, Knoop long diagonals >20 μm in length cover a wider range of steel hardness than do the mean Vickers diagonals for the same specimen hardness (Figure 6 plots the HRC equivalent hardness relative to the diagonal ratios of the equivalent HV and HK values). Note that when using a 50 gf load, the entire steel range, from 100 to 1000 HK, yielded long diagonals >20 μm. But, when a 25 gf test load is used, only steels from 100 to 889 HK exhibit long diagonal lengths >20 μm. And, when a 20 gf load is used, only steels from 100 to 711.5 HK exhibit long diagonal lengths >20 μm. If a 15 gf load is used with the Knoop indenter, only steels with a hardness from 100 to 533.6 HK will exhibit long diagonals >20 μm. If a 10 gf test load is employed with the Knoop indenter, only steels with a hardness from 100 to 355.7 HK will exhibit long diagonals >20 μm. On the other hand, when a 50 gf load is used with the Vickers indenter, only steels with a hardness from 100 to 231.8 HV exhibit mean diagonal lengths >20 μm. At a test force of 25 gf using the Vickers indenter, only steels with a hardness from 100 to 115.9 HV exhibit mean diagonal lengths >20 μm. This clearly shows that the Knoop indenter has greater usefulness than the Vickers indenter at test forces ≤50 gf.
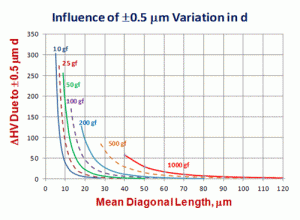
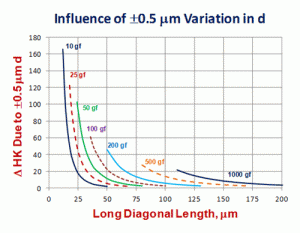
In general, most metallographers cannot repeatedly measure indent diagonals in tests performed with a substantial time break between measurements with a precision better than about ±0.5 μm. So, if we calculate the Vickers or Knoop hardness as a function of test load and diagonal length, where we determine the hardness difference between minus 0.5 μm versus plus 0.5 μm of a given diagonal length, we can see how this degree of imprecision in the diagonal measurement will affect the reported hardness value. Figure 7 shows a plot of the mean diagonal length versus the difference in Vickers hardness for minus 0.5 μm and plus 0.5 μm as a function of test force. Figure 8 shows a similar plot for Knoop hardness. Figure 7 shows a strong detrimental error in Vickers hardness for mean diagonals <20 μm for loads ≤50 gf. In comparison, Figure 8 shows less imprecision at all test forces and diagonal lengths, compared to Figure 7 for the Vickers test, at test forces <100 gf. This work shows the need for correlations between Knoop hardness as a function of test forces <500 gf so that the greater precision in measuring Knoop indents as test forces <100 gf can be better utilized. Presently, the only correlation between Knoop and other test scales is available only for a 500 gf (“and greater”) test force.
 |
 |
| Figure 7: Influence of a ±0.5 μm measurement imprecision in measuring the mean Vickers diagonals upon the possible variation in Vickers hardness as a function of test force and mean diagonal length. | Figure 8: Influence of a ±0.5 μm measurement imprecision in measuring the long Knoop diagonal upon the possible variation in Knoop hardness as a function of test force and mean diagonal length.
|
Conclusions
It is quite obvious from this study that E384 and the newly proposed E92 should not recommend performing micro-indentation tests at test forces <25 gf down to 1 gf. Very low test forces simply do not yield indent lengths that can be measured with adequate precision. Because the long Knoop diagonal for the same specimen and hardness is ~2.7 times longer than the mean Vickers diagonal, the Knoop test can be utilized to test steels down to a test force of 20 gf while the Vickers indenter really should not be used at test forces<50 gf. The light optical microscope simply does not have adequate resolution to measure indents smaller than ~15 μm in length even when a 100X, 0.95 NA objective is employed – which is rarely available for most micro-indentation hardness testers.
George Vander Voort has a background in physical, process and mechanical metallurgy and has been performing metallographic studies for 47 years. He is a long-time member of ASTM Committee E-4 on metallography and has published extensively in metallography and failure analysis. He regularly teaches MEI courses for ASM International and is now doing webinars. He is a consultant for Struers Inc. and will be teaching courses soon for them. He can be reached at 1-847-623-7648, EMAIL: georgevandervoort@yahoo.com and through his web site: www.georgevandervoort.com
To View a listing of all George’s articles please click here
Read George Vander Voort’s Biography