As in any discipline, understanding the underlying scientific principles has profound practical implications when properly understood. In this series of articles, we will review the first principles of vacuum technology and explain them using real-world illustrations. Most industrial vacuum systems can, in broad-based terms, be categorized in terms of low (i.e., “soft”), medium, high (i.e., “hard”) and ultra-high vacuum (Table 1). These ranges are very useful in describing the various pressure, flow, and other phenomenon encountered, which leads to a better understanding of vacuum pump selection and operation, and system operational requirements at the different vacuum levels.
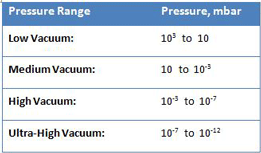
As shown by the difference in pressure from low to ultra-high vacuum, industrial vacuum systems must operate under an extremely wide range of pressure. In fact, the range is so large it is hard to actually comprehend. Consider a volume of gas at a pressure of 1000 mbar (atmospheric pressure) in a 1 meter by 1 meter by 1 meter container sealed so that no molecules can escape or enter. It is easy to understand that if the container is expanded in volume while still remaining sealed, the pressure will decrease (and a vacuum will be created) in direct proportion to the increase in volume (in accordance with Boyle’s law). If, for example, the container volume is doubled to 2 cubic meters, the pressure will decrease by half, to 500 mbar. When this relationship is expanded to the scale of industrial vacuum systems, the result is striking. If we take this same 1 cubic meter volume of gas and increase its volume sufficiently for the pressure to be reduced to 10-12 mbar (ultra-high vacuum), the container will be a staggering 99 km long x 99 km wide x 99 km high, or 200 times the volume of the grand canyon!

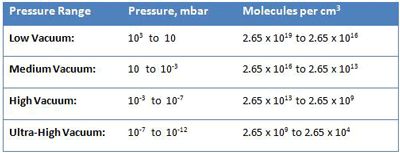
Another way to understand the operating pressure range of industrial vacuum systems is to consider gas density or the number of gas molecules that reside in a given volume. There are roughly 2.65 x 1019 or 26,500,000,000,000,000,000 molecules in a cubic centimeter of gas at 103 mbar, which is atmospheric pressure at sea level (Table 2). Under lower and lower pressure, the molecules spread out further and further, until, at ultra-high vacuum (10-12 mbar), there are only 2.65 x 104 or 26,500 molecules per cubic centimeter. At this density, there is only one molecule roughly every 0.33 mm in space. Since the diameter of each gas molecule is much less than this (4 x 10-8 cm for air, for example), there is a great deal of space between molecules. To put it into proportion, if gas molecules were grains of sand, at ultra-high vacuum they would be 1,650 meters apart. At these extremely low pressures, the collisions between molecules, which normally dictate the properties of gases, become very infrequent and a different theoretical model is required to explain their properties (the so-called Kinetic Theory of Gases).
The Continuum Theory and The Kinetic Theory of Gases
At or near atmospheric pressure, and in non-vacuum systems, the so-called continuum theory accurately describes the properties of gases. In simple terms, it tells us that collisions between gas molecules dictate the properties of a gas. The continuum theory is what we call macroscopic in nature, and governed by the gas laws such as The Ideal Gas Law, Boyles Law, and Daltons Law.
- Ideal Gas Law: In a perfect or ideal gas the change in density is directly related to the change of both temperature and pressure
- Boyles Law: The pressure exerted by a given mass of an ideal gas is inversely proportional to the volume it occupies, at constant temperature
- Dalton’s Law of partial pressures: In a mixture of non-reacting gases, the total pressure exerted is equal to the sum of the partial pressures of the individual gases
After vacuum pump technology developed to the extent that fewer and fewer gas molecules were possible in a given volume, the governing principles affecting the properties of these gases changed, and molecular considerations became primary. Namely, the gas molecules become so spread out that intermolecular collisions between gas molecules no longer dominated, but rather collisions with the chamber walls were the determining factor affecting the gas properties. This led to the Kinetic Theory of Gases, which applies not only at low pressures (high vacuum) but is also accurate over the entire range of pressures seen in industrial vacuum systems.
Molecular Density and Mean Free Path
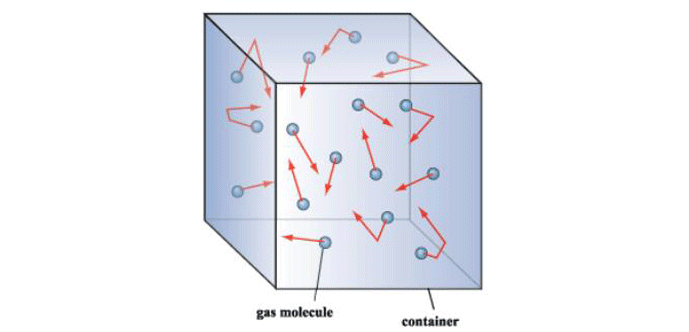
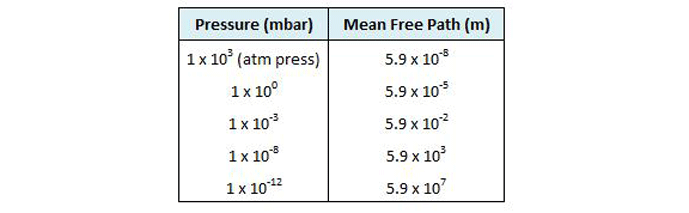
The primary concept of the kinetic theory is that a gas consists of a great number of individual particles (molecules) each moving individually and randomly and that the collisions between them, as well as their collisions with the vessel walls, determine the pressure created by the gas. The molecular density, or the number of gas molecules per unit volume (Table 2), varies in proportion to pressure. Further, the mean free path (or the average distance a molecule must travel before colliding with another molecule) increases greatly as the pressure decreases (Fig. 2). Most importantly, the increased mean free path at reduced pressure dictates that molecular collisions with the vessel walls govern the gas properties at reduced pressure.
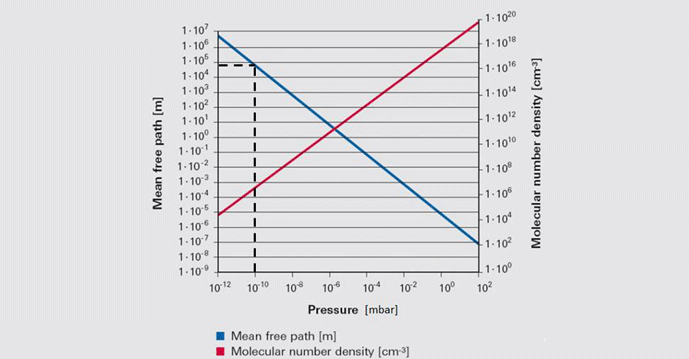
Note in this figure that at an ultra-high vacuum of 10-10 mbar the mean free path is nearly 105 or 100,000 meters. This means that collisions between gas molecules are so infrequent that each molecule has to travel an average of 100,000 meters before a chance collision with another molecule. Since the sides of the vessel are much closer than this, collisions with the vessel wall are much more frequent than with other molecules. For this reason, at high and ultra-high vacuum molecular collisions with the walls of the vessel (Fig. 3) dictate the pressure exerted by the gas on the walls of the vessel.
This understanding leads to the formulation of gas pressure as a function of gas density, (mean square) velocity, and mean free path of the individual gas molecules. With this foundation, referred to as the Kinetic Theory of Gases, calculations of pressure, flow, and conductance over the entire vacuum operating range are derived.
The kinetic gas theory is based on the following five assumptions.
- Gases are comprised of a large number of particles that behave as inelastic, spherical objects in a state of constant, random motion.
- The particles move in a linear manner until colliding with another particle or the walls of their container.
- The size of the particles is negligible in relation to the space between them and therefore most of the gas volume consists of empty space.
- There is no force of attraction or repulsion between gas particles or between the particles and the walls of their container and thus their total energy is simply equal to their kinetic energies.
- Collisions between gas particles and collisions with the container walls are 100% elastic. None of the energy of a gas particle is lost when it collides with another particle or with the walls of the container.
Considering the above assumptions, we can derive a formula (Equation 1) to describe the pressure of a gas under the kinetic gas theory.
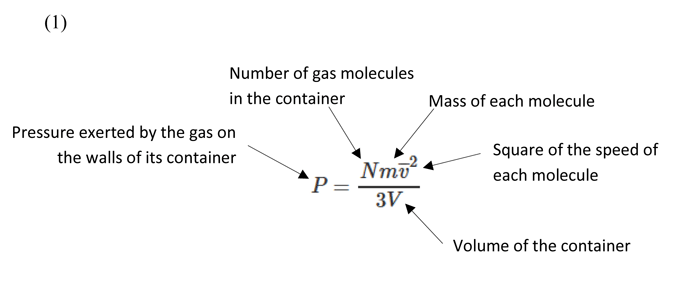 The above is related to the principle in classical mechanics where kinetic energy = 1/2 m v2, developed by Leibniz and Bernoulli and originally described in 1722 by Gravesande in a series of experiments in which brass balls were dropped from varying heights onto a soft clay surface. Gravesande found that a ball with twice the speed of another would leave an indentation four times as deep, from which he concluded that the force generated by a body in motion is proportional to the square of its velocity. This same principle applies to the kinetic gas theory where the force of the molecules impacting the walls of the vessel is what generates the gas pressure, in proportion to the square of their speed.
The above is related to the principle in classical mechanics where kinetic energy = 1/2 m v2, developed by Leibniz and Bernoulli and originally described in 1722 by Gravesande in a series of experiments in which brass balls were dropped from varying heights onto a soft clay surface. Gravesande found that a ball with twice the speed of another would leave an indentation four times as deep, from which he concluded that the force generated by a body in motion is proportional to the square of its velocity. This same principle applies to the kinetic gas theory where the force of the molecules impacting the walls of the vessel is what generates the gas pressure, in proportion to the square of their speed.
As an example, it is useful to consider nitrogen, since air is mostly made up of nitrogen. Each individual nitrogen molecule in a closed container is rapidly moving in a straight line, until bouncing off another nitrogen molecule or off the container wall, essentially like a bunch of billiard balls. At a gas temperature of 20° C, each individual nitrogen molecule travels at an average speed of 518 meters per second, or 1,864 km per hour. Although each molecule is tiny, the cumulative impact force generated from all the molecules striking our skin each second (roughly 3 x 1027 per square meter) is the pressure of ordinary air on our bodies.
In actuality, the gas molecules in a system move at a wide range of velocities, but the average (mean) velocity is used for the purposes of calculating pressure and other effects. In other words, molecules of the same gas exhibit a distribution of speeds (Fig. 4), with the mean represented by the peak of the curve. Some move faster, and others slower.
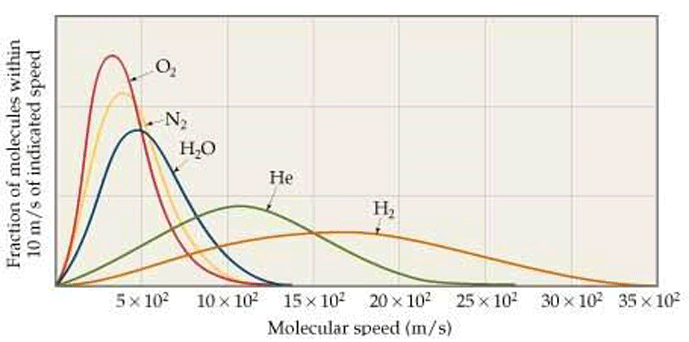
There is an interesting consequence of the distribution of molecular speeds in a gas. Due to the bell-shaped curve of the speed distribution, there are significant numbers of molecules with a speed much faster (about 6 times faster) than the average. The escape velocity from earth for any moving object (including gas molecules) is 11.2 kilometers per second. The fastest nitrogen molecules will travel 518 × 6 = 3108 meters per second. This is well under the escape velocity and therefore nitrogen does not escape earth’s gravity.
On the other hand, hydrogen molecules in the Earth’s atmosphere will move as fast as 2700 × 6 = 16,200 meters per second or 16.2 kilometers per second. This is above the earth’s escape velocity. So the fastest hydrogen atoms, those in the tail of the distribution, are energetic enough to overcome the grip of gravity. Hydrogen will, therefore, escape into space, as will helium. Earth’s gravity retains heavy gases but lighter gases drift into space.
In the article above, we talked about the Kinetic Theory of Gases and how it can be used to calculate gas properties. We also considered the relationship between molecular density, mean free path, molecular velocity, and pressure. Now we turn our attention to a discussion about temperature and kinetic energy, pressure and kinetic energy, and types of flow in vacuum systems. Again, we will focus on the basics, using fundamental comparisons to explain the concepts significant to industrial vacuum systems.
The relevance of Temperature to the Kinetic Theory of Gases
Based on an atomic understanding of the world we live in, the Kinetic Theory reveals that gas properties are highly dependent on the speed of their molecules, which determines their kinetic energy, and therefore the gas pressure. When considering the effects of the Kinetic Theory, it is also important to understand the influence of temperature. Specifically, the speed of the molecules in a gas is dependent on its temperature (the higher the temperature the faster the gas molecules move). Another way to think of it is that the temperature of a gas is a measure of the average kinetic energy of that gas.
According to Kinetic Theory, a gas consists of a large number of tiny molecules, all in constant random motion, elastically colliding with each other and the vessel that contains them. Pressure is the net result of the impact force of those collisions against the vessel wall. The speed of the molecules during this motion is not random at all, but follows a bell curve, with a predictable distribution about the average. The molecular speed is dependent on the weight of
the molecules and their temperature, or inherent heat energy. So for a given gas, the heat energy contained in its molecules determines their energy level and therefore their speed.
In order to fully appreciate the influence of temperature on a gas, it is useful to understand degrees Kelvin (more correctly defined simply as Kelvin), which is an absolute temperature scale (degrees above so-called absolute zero where all motion stops). This is a true measurement of kinetic energy. As there is no temperature less than zero, and no volume less than zero, absolute zero is the lowest temperature possible, where all kinetic motion stops, and the gas’s volume is reduced to zero.
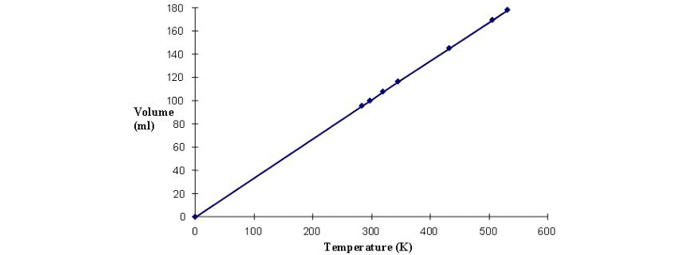
This is borne out when the volume of a gas at several different temperatures is measured and plotted (Fig. 1). When the graph is then extended to 0 K, the volume goes to zero. Keep in mind the gas molecules do not individually have zero volume, but the space between molecules approaches zero. Although absolute zero has never been attained, temperatures as low as a billionth of a kelvin have been achieved on small samples. For comparison between units, bear in mind the relationship between K and °C whereby absolute zero equals -273.16°C (−460.67°F). With an understanding of absolute temperature, we can discuss the effects of temperature on gas volume and pressure.
It can be seen that for a given gas, as its temperature is increased, the average velocity of its molecules increases in proportion to the square root of its absolute temperature. Take nitrogen for example (Fig. 2). At 300 K (27° C or 81° F) its molecules are traveling an average of 400 meters per second (1,312 feet per second or 894 MPH). When the absolute temperature is increased by a factor of 4, to 1,200 K (927° C or 1,700° F), its average molecular speed increases by a factor of 2 (which is the square root of 4), to 800 meters per second (2,624 feet per second or 1,789 MPH).
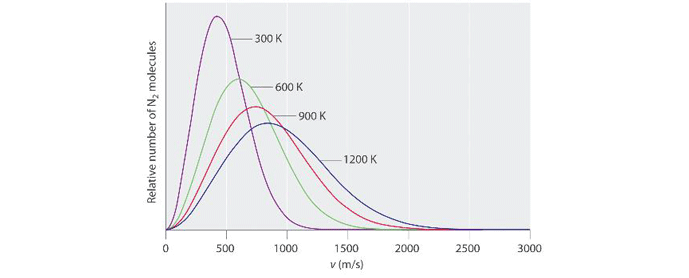
Also note on figure 2 that at lower temperatures, the curves are narrower and taller. At higher temperatures, there is a wider distribution of energy levels (and corresponding molecular velocities) among the population of molecules. At lower temperatures, there is less variability between the velocities of different molecules and so the curve is narrower at its base. When the (absolute) temperature of a gas is understood to be a measure of its kinetic energy, the implications of the Kinetic Theory of Gases in regard to temperature become clear. Recall that under the Kinetic Theory of Gases, the pressure exerted by a gas is the sum total of the force exerted by all the physical impacts between the gas molecules and the vessel (or vacuum chamber, or vacuum piping, etc.) containing it. Since the velocity of the molecules is directly related to (the square of) temperature, the pressure of the gas is therefore also directly related to temperature, by the square root of its absolute temperature.
The effect of temperature on pressure as described by kinetic theory can be illustrated by a simple experiment using a party balloon and liquid nitrogen (Fig. 3). When the inflated balloon is temporarily submerged in a container of liquid nitrogen, which is at a temperature of 77 kelvin (-196 °C or -320° F), the air molecules inside it immediately drop in temperature and lose kinetic energy (i.e. their speed decreases). As a result of the decrease in molecular speed, two things happen; (a) the collisions between molecules become less frequent, allowing the space between them to decrease, and (b) the force with which the molecules collide with their container (the balloon) decreases, reducing the pressure the air exerts on the balloon. This causes the balloon to shrink. The reduced volume of the air is proportional to its absolute temperature. Since the temperature of the air inside the balloon was decreased from 293 K (20° C, room temperature) down to 77 K, the resulting volume is 77/293 = 26% of the balloon’s original volume.

Types of Flow in Vacuum Systems; Continuum, Molecular and Knudsen
The manner in which a gas flows in a vacuum system is dependent on the gas pressure. At rough vacuum pressures above approximately 1 mbar (.015 PSI), continuum (or viscous) flow prevails. At these pressures, the molecules are relatively close together, and their collisions more frequent. Therefore flow is governed by interaction between molecules. As a result, the entire volume of gas, or group of molecules can be made to move in an ordered motion, that is flow (Fig .4). This ordered motion is superimposed, or added to, the normal random motion of the individual molecules. The gas at these pressures can be thought of as having a viscosity, or stickiness, that permits their ordered motion due to the internal friction between molecules. Therefore the preferred speed and direction of molecule flow will be the same as for the macroscopic gas flow.

Molecular flow, on the other hand, is seen at pressures below .001 mbar (.000015 PSI), which is in the high and ultra-high vacuum range. At these pressures, intermolecular collisions are much less frequent due to the fact that there is so much space between gas molecules (Fig. 5). Molecules move freely without any mutual interference, and therefore there is no ordered group flow possible. The molecules individually move in a straight line without colliding, until they strike the wall of the vessel or pipe containing them. Molecular flow is present where the mean free path length (average distance a molecule must travel before colliding with another molecule) is much larger than the diameter of the pipe the gas is flowing through and therefore the molecules are free to travel until they collide with the pipe walls. As a consequence, a gas particle can move in any arbitrary direction in a high vacuum and macroscopic, continuum flow is no longer possible.

In the transitional range between continuum flow and molecular flow, Knudsen flow prevails. In this range both wall collisions and intermolecular collisions are influential in determining flow characteristics.
Pump Technology In The Continuum and Molecular Flow Range
Vacuum pumps that operate in the continuum (viscous) flow range such as roots blowers, screw pumps, claw pumps and rotary vane pumps function by moving the molecules as a group. They have the advantage of using the interactions between molecules (the viscous quality of the gas) to their advantage. They create a suction to draw the volume of gas to the pump inlet, then push it through the pump mechanism, and expel it at atmospheric pressure. As a result they can generate a high throughput and provide a quick drawdown in the roughing and low vacuum phases.
Pumps used to create high and ultra-high vacuum include diffusion pumps, cryogenic pumps, and ion pumps and must operate in the molecular flow range. They therefore use different technology than roughing and low-vacuum pumps. Since there is no true macroscopic flow in the molecular range, the pumps used at high and ultra-high vacuum cannot “pull” the gas out of the vacuum chamber. Rather their mode of operation is to simply capture the molecules that randomly enter the pump inlet. As a result, when the chamber pressure reaches the high and ultra-high vacuum ranges, the drawdown becomes much slower and the pump’s job becomes more difficult.
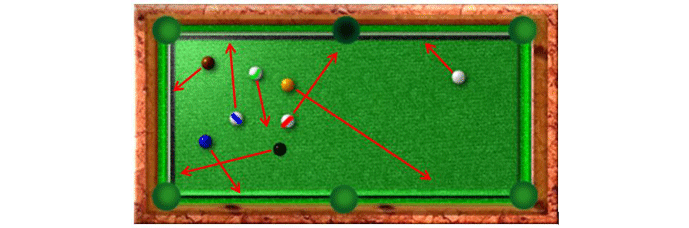
In order to understand the operation of a pump in the molecular flow range it is useful to imagine the molecules in a vacuum chamber as billiard balls on a pool table (Fig. 6) that has only one open pocket, which simulates the pump inlet. If the balls are all set in motion in random directions, such as after a break, but are allowed to keep bouncing off the bumpers without slowing down (as gas molecules do after colliding with the chamber walls), some of them would begin to fall into the pocket. Since the pocket does not have the ability to “pull” the balls toward itself, it relies on the chance occurrence that a ball will fall into it. At first, while more balls are present, there is a high probability that a ball will fall into the pocket, and the balls are removed rather quickly. As more of the balls fall into the pocket, there are fewer and fewer of them remaining, reducing the likelihood of a ball falling into the pocket. Eventually there are only a few balls left, and the probability of a ball falling into the pocket becomes very low. At this point, further ball removal is very unlikely and for practical purposes, no more balls will be removed in a reasonable amount of time. The equivalent of ultra-high vacuum has been attained.
Earlier in this article, we talked about the Kinetic Theory of Gases and in particular, we showed how the movement of atoms affects principles such as molecular density, mean free path, and molecular velocity and how they are used to analyze the macroscopic properties of gases such as pressure, temperature, and flow in a vacuum environment. Below we will discuss the related topic of gas flow, gas speed, conductance, diffusion, and effusion once again focusing on the fundamental concepts.
The speed of Gas Flow
When designing and using vacuum systems, it is critical to be able to predict the time required to draw the pressure down to the desired level. Since this time is directly related to the speed of the gas flowing through the system, it is therefore important to understand what influences the speed of gas flow. Of practical importance is the influence of pipe diameter, pipe bends, and devices such as filters and condensers. Flow phenomena are not easily understood unless the differing properties of the gas in the so-called continuum and molecular flow ranges are taken into account.
Choked (Blocked) Flow
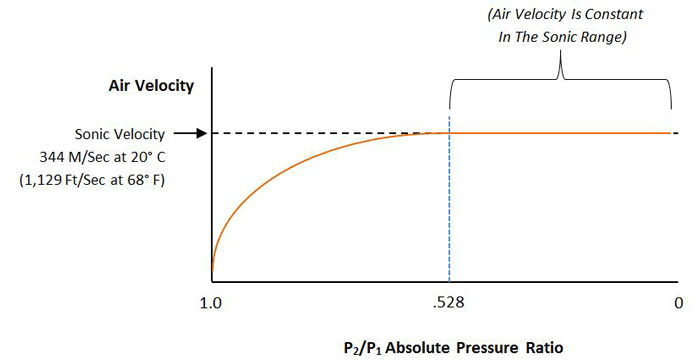
At low flow rates in the continuum, or viscous range of gas flow (occurring at pressures above roughly 1 mbar), the flow rate through a pipe or orifice is directly proportional to the pressure differential across the pipe or orifice. This changes when the flow speed of the gas reaches the speed of sound, referred to as the sonic velocity (approximately 1,223 km/h or 760 miles per hour), which is the speed of sound in that gas.
Increasing the pressure further will not increase the flow rate (Fig. 7). This condition is referred to as choked flow. Choked flow occurs when the pressure differential across the orifice, or through the pipe, is such that the pressure on the ratio between the high-pressure side and the low-pressure side of the orifice reaches a certain value specific to that gas. For air this value is 52.8% (PIN / POUT = 0.528).
This is of critical importance when venting a vacuum chamber. When the vent is opened, air at atmospheric pressure flows into the chamber at no greater than sonic velocity, no matter how low the pressure is inside the chamber. As venting continues and the chamber fills with gas, the pressure inside the chamber rises until it reaches PATM x 0.528, or 528 mbar (7.76 psi). After the pressure ratio rises above this point, the flow rate becomes proportional to the pressure difference across the vent. The takeaway is this – since the velocity of gas flow cannot be increased above sonic speed, the only way to increase the venting speed of a chamber is by using a larger vent.
Conductance
Conductance is the characteristic of a vacuum component or piping to “conduct” the gas through the system. Analogous to electrical systems, where the conductivity of a wire permits the flow of electrons through a circuit caused by the electrical potential, conductance in a vacuum system permits the flow of gas molecules through a vacuum system caused by the pressure differential generated by the pump. Conductance must be closely considered when selecting the vacuum pump and other components, to prevent reduced pumping rates and extended drawdown times. The capacity of the pump must be increased to accommodate the resistance or the inverse of the conductance.
Conductance has units of volumetric flow rate divided by pressure drop, expressed as liters per second or cubic feet per minute. The conductance between two points is defined as the gas flow rate flowing through a device divided by the resulting pressure drop.
Conductance is greatest in the viscous flow region (Cv), smallest in the molecular flow region (Cm), and in between in the transitional flow region (Ct). In other words, Cm < Ct < Cv. The flow resistance (the reciprocal of conductance) is greatest in the molecular flow range, at higher vacuum, and lowest in the viscous flow range, at lower vacuum. This may seem counterintuitive since gas is denser at higher pressures and less dense at higher vacuum. Why would a gas be easier to pump when in a denser state, and harder to pump while in a less dense state? The answer lies in the interaction of the gas molecules in the viscous flow vs molecular flow ranges.
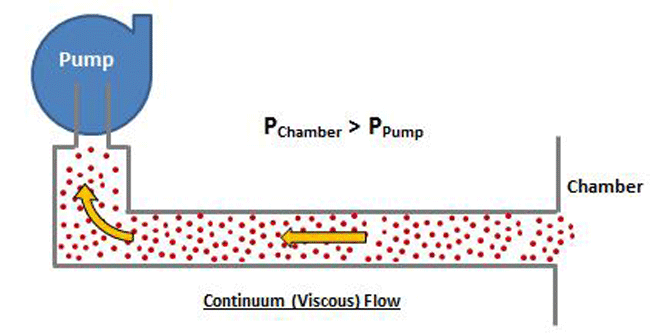
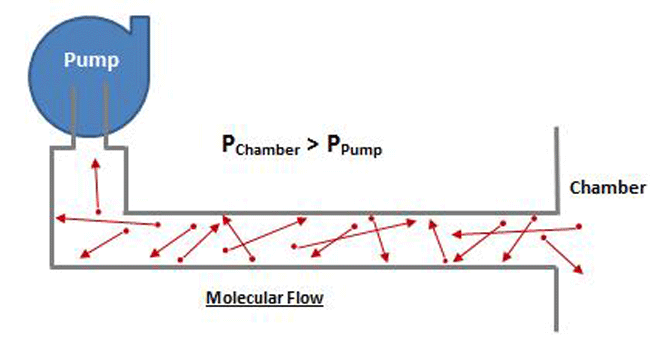
At higher pressure, which is where viscous flow occurs, the gas molecules are relatively close together and move collectively as a group. Note that in Figure 8 the chamber pressure is greater than the vacuum pump inlet pressure. In the viscous flow range, collisions between molecules are frequent, since they are relatively close together, and when a pressure differential is exerted, the molecules move as a group. In the molecular range, on the other hand (Fig. 9), the molecules are so spread out that collisions are very infrequent. Therefore when a pressure is exerted on the chamber end of the pipe, the molecules can’t “push” each other through the pipe because they almost never collide, but rather move independently. The pump must rely on the random motion of the molecules to enter the pump inlet, at which time they are simply captured. The pump does not have the ability to draw the molecules toward it.
A few essential facts about conductance worth reviewing:
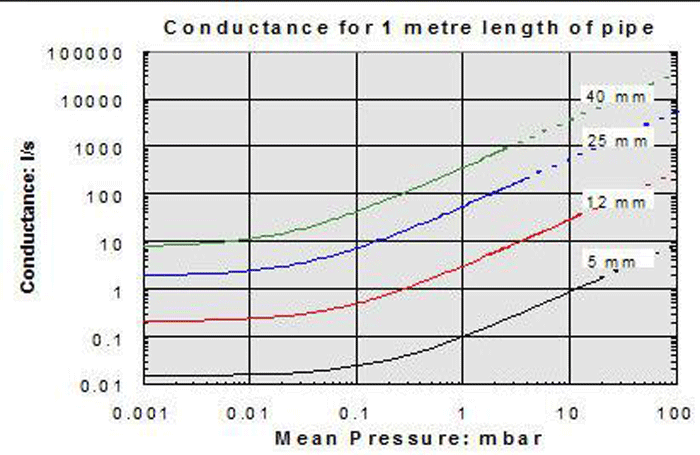
1. Conductance can be calculated for a system. Pipe conductance is commonly taken from charted values and is dependent on pipe diameter, pipe length, flow rate, and pressure. Conductance values for components such as valves, filters, and traps are published by their manufacturers and are based on empirical values.
2. Conductance changes during the three modes of flow through the system: continuum flow, molecular flow and Knudsen flow (the transition between the two). Recall that continuum flow occurs at higher pressure (low vacuum), and molecular occurs at lower pressure (high vacuum). Therefore the conductance of a given vacuum component is not a constant value but varies with the system pressure. When calculating conductance, therefore, it is necessary to realize that only the conductance values applicable to a certain pressure range may be applied in that range.
3. In order to select a vacuum pump, it is necessary to calculate the total conductance of the system being designed. This is usually done as an approximation, with a safety factor added. The pump can then be selected to provide the desired flow rate in each pressure range and the cumulative flow determined over time.
4. In the molecular flow region, the conductance value is independent of pressure (Fig. 10). The curves flatten out in the lower pressure range. In other words, at high and ultra-high vacuum the conductance remains constant at different pressures. This is not the case in the continuum and Knudsen ranges, where conductance is highly dependent on pressure.
5. System Geometry:
a. Shorter length and larger diameter piping are best
b. Manifold and piping diameter should be the same as, or greater than, the inlet to the vacuum pump
c. The pumping system should be physically located as close as possible to the chamber
d. The number of bends, elbows, and turns should be kept to a minimum
Effusion
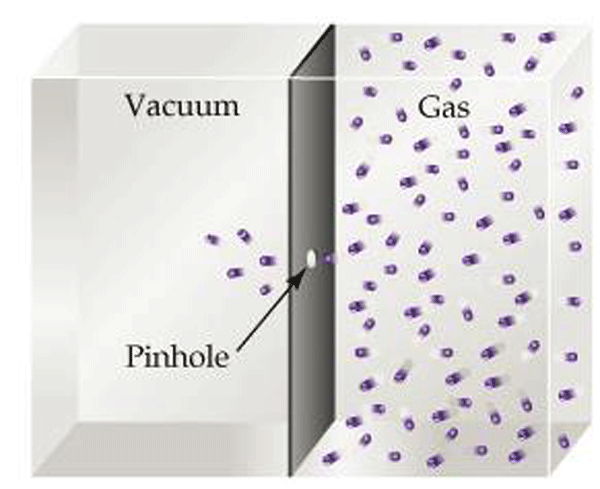
Effusion describes the manner in which gases to pass through a small hole from a region of higher pressure to lower pressure (Fig. 11). It is relevant to vacuum systems because it explains the action of vacuum leaks under high vacuum conditions when molecular flow prevails.
In order to understand effusion, consider a barrier between an area of low pressure (high vacuum) and of high pressure (Fig. 11). If a very small (diameter smaller than the root mean path) pinhole is created in the barrier, the kinetic motion of the gas molecules dictates that molecules will pass through the hole when their path randomly directs them through it. Recall that the root mean path (Table 1) is the distance a gas molecule travels before colliding with another molecule. The root mean path varies greatly over the pressure range that vacuum systems operate. Since at high vacuum any hole or leak in a vacuum system is smaller than this distance, the gas will not flow through the hole in ordered, group motion. Rather, over time this random motion causes some particles to eventually pass through the hole.
Graham’s laws dictate that the effusion rate of a gas is greater for lighter gases than heavier gases. This is due to the fact that lighter molecules move faster. Since the only way for a molecule to escape from its vessel is for it to “hit” the hole, the faster the molecules are moving, the greater the likelihood that a molecule will hit the hole and effuse. Therefore hydrogen and helium, which have low molecular weight and high velocity, will pass through a leak much faster than air.
Effusion can also be used to describe the manner in which molecules enter a high vacuum pump. Since the diameter of a vacuum pump will be greater than the mean free path for pressures below about 10-4 mbar, essentially all molecules which arrive at the inlet continue and pass into the pump because collisions between molecules in the region of the inlet are negligible. The term effusion also helps clarify the manner in which high vacuum pumps collect the molecules that enter the pump, rather than suck the molecules toward the inlet. The molecules could be said to effuse through the pump inlet.
Diffusion
According to the Kinetic Theory of Gases, gas molecules are in a constant state of random motion, moving at varying speeds and in many different directions. Because of their kinetic energy at temperatures above absolute zero, all particles undergo diffusion or movement from an area of high concentration to one of low concentration. The rate of this movement is related to temperature, the viscosity of the medium, and the mass of the molecules. Diffusion causes the gradual mixing of different gases.
The principle of diffusion has relevance to the field of vacuum technology in a couple of ways. First, diffusion is the means by which gas molecules pass through a solid material to contaminate a vacuum process. Even if the components of a vacuum system could be designed with no physical leaks, as well as valves and other components that mechanically seal perfectly, small molecules such as helium can permeate polymer seals and even the metal walls of vacuum chambers. Various strategies are used to overcome this, including relying on the vacuum pump to simply remove the invading molecules, and using materials with better permeation constants.
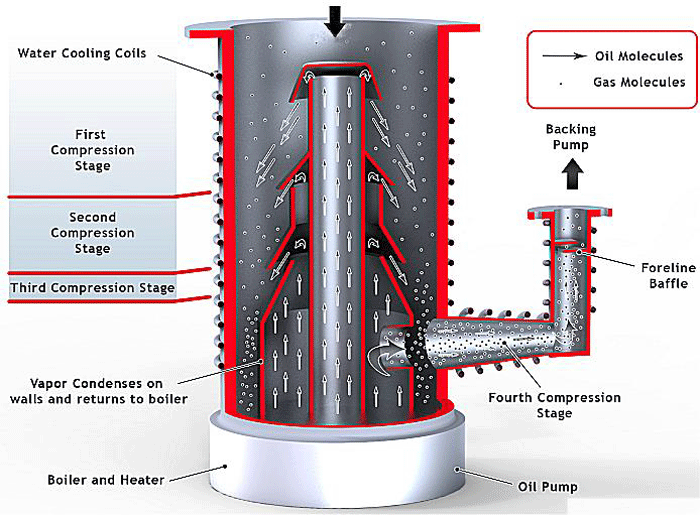
The other relevance of diffusion in vacuum systems involves the diffusion pump (Fig. 12), which is commonly used to achieve a high vacuum. Its principle of operation relies on diffusion of the molecules of pumped gas into the pump media, such as oil or polymer. As discussed previously, all high vacuum pumps rely on the capture of the gas molecules, and diffusion pumps are able to capture the molecules by maintaining a low concentration of gas molecules diffused in the pumping media. The molecules of pumped gas are then removed from the media through condensation, and this cleaned media is constantly reintroduced, which induces further diffusion of the gas by preventing the media from becoming saturated with the gas.
References
- www.grayline.com
- http://web2.uwindsor.ca/courses/physics/high_schools/2005/Brownian_motion/kinetictheory.jpg)
- http://wps.prenhall.com/wps/media/objects/3311/3391331/blb1008.html).
- The Ideal Gas Law
- http://2012books.lardbucket.org/books/principles-of-general-chemistry-v1.0/s14-07-the-kinetic-molecular-theory-o.html
- http://www.thesciguys.ca
