Vacuum gauges all measure the pressure readings in the range from atmospheric pressure down to some lower pressure approaching absolute zero pressure, which is not attainable. Some gauges read the complete range and others can only read a portion of the range, usually used for very low pressures.
If you have a typical vacuum furnace it is normal to have at least three electronic vacuum gauge heads mounted on the system to monitor the level of vacuum at selected positions. These gauge heads send signals back to the controls system and the vacuum readings are used to ensure that the vacuum pumps are working correctly and that the process chamber is at the correct low pressure (vacuum) for the specific process. To many casual observers, the readings and names of the measuring units being used are like a foreign language, and they may well be because many names were derived in Europe. Let’s take a look at the different vacuum measurement units in use around the world and where the names came from.
Torricelli, Pascal and the mercury barometer
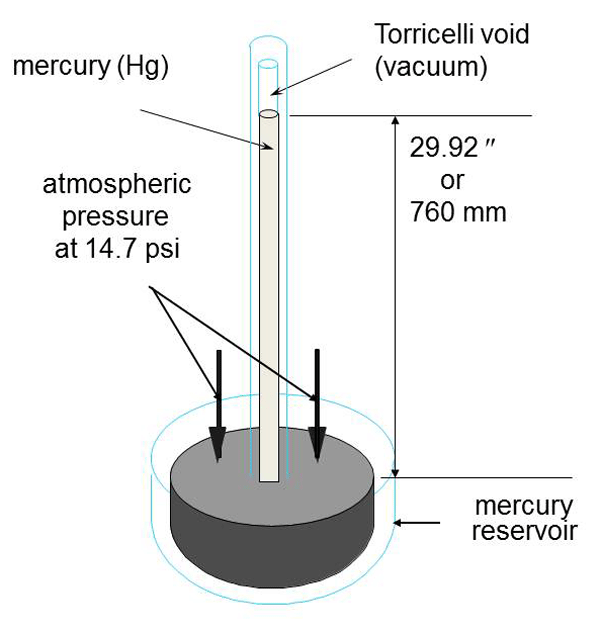
The understanding that pressures lower than the surrounding atmospheric pressure existed started around the 1640s in Italy. In 1643 Torricelli developed what was to become the mercury (chemical symbol Hg) barometer. He found that atmospheric pressure would support a column of mercury about 30 inches high in a glass tube with one end closed. (Fig. 1) His research was developed from previous experiments by Gasparo Berti using water as the liquid. The use of mercury (not then known to be a hazardous material) made the equipment much more compact due to the relative density of mercury being 13.95 times that of water. Torricelli took a long glass tube with one end closed and filled it with mercury. He then closed off the open end and inverted the tube into a container of mercury. When the closure was removed, possibly a fingertip, the mercury level inside the tube dropped until it stabilized at a measurement of close to 30 inches above the mercury level in the container. The open volume in the top of the glass tube was the subject of much discussion at the time because no one knew if there was anything in that “Torricellian void” as it became known. Unfortunately, Torricelli died only four years after the mercury barometer experiment and I have often wondered if mercury poisoning could have been involved.
Blaise Pascal was another early scientist who lived in France. In 1647, having heard of Torricelli’s mercury in a closed tube demonstration, showed that the height of the column of mercury varied at different altitudes by taking a reading at several points on a hill near his home.
Mercury vacuum gauges
From this barometer, a simple mercury vacuum gauge can be developed that indicates the pressure level as linear measurement, the difference between the levels of mercury in the container and in the glass column.
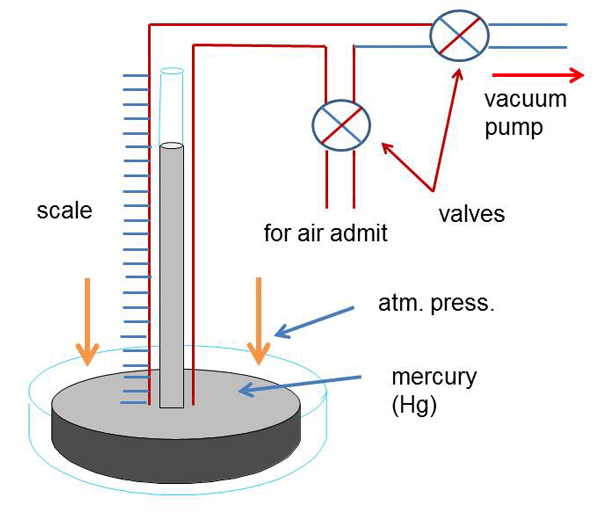
For example, if the closed glass tube in Fig. 1 is replaced with a graduated open-ended tube that has a shut-off valve, air-admit valve and a nozzle fitted to it, the top of the tube can now be connected by a vacuum hose to a vacuum pump. (Fig. 2) Initially, with the shut-off and air-admit valves open and the vacuum pump switched off the mercury level in the glass tube would be at the same level as the rest of the mercury in the container. The system is all at atmospheric pressure. When the shut-off and air admit valves are closed and the vacuum pump switched on the vacuum line is evacuated from the vacuum pump up to the shut-off valve. At that point the mercury level in the glass tube and dish are unchanged. The tube is still at atmospheric pressure but now contains a trapped volume of air due to the closed valves. When the shut-off valve is slowly opened, gas will move from the glass tube towards the lower pressure on the vacuum pump side of the valve and the pressure will drop in the glass tube. As the pressure drops in the glass tube, atmospheric pressure acting on the mercury in the container will push mercury up the inside of the tube due to the pressure differential. Reading the graduations on the side of the tube will tell you what the level of vacuum is.
If this was an actual demonstration we would now need to close down the system. First, the shut-off valve is closed isolating the vacuum pump from the measuring tube; next, the vacuum pump can be shut off. Then, when the air-admit valve is slowly opened, air will be admitted to the measuring tube and the mercury level will drop to its original level in the dish. Lastly, the shut-off valve should be opened to allow the inlet side of the vacuum pump to return to atmospheric pressure.

This simple gauge measures the difference in the levels of the mercury from 0 inches at atmospheric pressure up to 29.92 inches of Hg at the best vacuum attainable. This scale is still in use today, usually shown as 0 to 30 inches of Hg on gauges such a Bourdon dial gauges. Other measuring units have become more popular due to the need to measure very low pressures that cannot be resolved on a 0 to 30 scale.
Vacuum measuring units
I have found some confusion over the years talking about “vacuum units”. In some parts of the English speaking world, a “unit” is also what others call a “system”, so a “vacuum unit” to them is a vacuum pump with some valves and other components mounted to it. Now I am careful to say “vacuum measuring units” in an attempt to make it clearer to everyone. From the original Torricelli experiments we have already learned of two vacuum measuring units, but here I include another one that most non- vacuum readers will also be familiar with. In all cases, zero represents absolute zero pressure (not attainable, even in outer space) and the number represents standard atmospheric pressure in the units shown.

1) Pounds per square inch absolute (psia) on a scale of 0 to 14.7
2) Inches of mercury (Hg) on a scale of 0 to 30, and the metric equivalent
3) Millimeters of Hg on a scale of 0 to 760 (A millimeter = 1/1000th of a meter)
One needs to be cautious here, as the original mercury in a tube vacuum gauge measures the reduced pressure (vacuum) from atmospheric pressure downwards towards zero pressure, but the numbers on the scale read from 0 towards a maximum of 30. This is called “gauge pressure” and will vary depending on the atmospheric pressure. Mechanical vacuum gauges such as the Bourdon dial gauge (Fig. 3) read from “zero” at atmospheric pressure down to a full-scale vacuum reading of 30 inches of Hg. As the pressure drops (or goes down) the vacuum reading number rises (or goes up). The Bourdon gauge shown in Fig.3 confuses things more by showing the inches of mercury as negative numbers. There can be no such thing as negative pressure; it is always a positive pressure but lower than atmospheric pressure.
Low pressure is equivalent to a high vacuum and vice versa. When writing about vacuum technology or vacuum systems it is important to use either pressure terms or vacuum terms consistently and not use both. Generally expressing everything in terms of pressure is preferred.

A scale of 0 to 30 inches of Hg does not allow for accurate measurements of the low pressure produced by oil-sealed mechanical vacuum pumps, but the metric equivalent of 0 to 760 mm of Hg does allow for more accurate readings because there are more divisions on the scale. However, when we start to talk about mm of Hg scales we also read the vacuum gauges as absolute pressure rather than as gauge pressure. Absolute pressure readings start at zero representing “absolute zero” pressure and read up to 760 representing standard atmospheric pressure in the case of the mms of Hg scale.
As vacuum pumps became more efficient it also became necessary to have a smaller vacuum measurement unit than the mm of Hg. This was only possible after the invention of electronic vacuum gauges because you really can’t see any divisions of a millimeter on a linear scale. The mm of Hg was divided into 1000 smaller parts which were called microns. The word micron means a one-millionth part of a meter. In some industries, electronic vacuum gauges are used that read in microns, for example from 1000 down to 0 microns which would be the same as from 1 down to 0 mm Hg. (See Fig. 4)
In the 1970s scientists decided that they did not want to measure low pressures in linear measurements such as microns and millimeters. In honor of Torricelli, they renamed the millimeter of Hg unit the torr. The symbol for the vacuum measurement unit torr is Torr, capitalized as is normal for metric units derived from names. This now gives us vacuum measuring units:
4) Torr, and standard atmospheric pressure = 760 Torr, and for smaller measurements
5) MilliTorr or mTorr, where 1 mTorr = 1/1000 of 1 Torr
In Europe, which measures most things in metric terms, the vacuum measurement unit in general use is the millibar or mbar.
6) Millibar, symbol mbar, where 1 mbar = 1/1000 of a bar, and standard atmospheric pressure is 1013.25 mbar
The bar scale where 1 bar = 1000 mbar is a very simple scale. The choice of 1013.25 mbar as standard atmospheric pressure was evidently chosen because it happened to be the typical atmospheric pressure in Paris.
The metric standards group System Internationale (SI) – based in Paris – or International Standards Organization (ISO) has also designated an SI vacuum unit based on the metric unit of force Newton/square meter (N/m2). The name chosen for this vacuum measurement unit was Pascal, another 1640s scientist.
7) Pascal, symbol Pa, where standard atmospheric pressure is 101,325 Pa. Note that 101,325 Pa is 100 times larger than 1013.25 mbar, so 1 mbar = 100 Pa.

Due somewhat to the fact that the ratio between 760 Torr and 1013 mbar is 3 to 4, making conversions easy, and at low pressures, the difference is almost unnoticeable (see Fig. 5) the mbar remains a popular measurement term even though the Pascal is always used in scientific papers. As time passes I’m sure that the SI vacuum measurement unit Pascal will slowly become more used in Europe even if the torr remains the main vacuum measurement unit in the USA. During my many years in Canada, I found that both torr and mbar units were used due to influences from US and European made vacuum equipment. Of course today, many electronic vacuum gauges can simply be switched to select the vacuum measuring unit that the user wants to see.
One other major difference in reading “gauge” scales and “absolute” scales is the change of the scale from linear to logarithmic. If you tried to use a linear torr scale from 0 to 760 and then divide each torr division into millitorr you would need a magnifying glass or better to see any reading, if at all. By using a logarithmic scale each section of the scale has good resolution to make an accurate reading off the scale. For example from 760 to 100, 100 to 10, 10 to 1, 1 to 0.1, 0.1 to 0.01, 0.01 to 0.001 in the case of Convection and Pirani gauges. See the torr and mbar scales on Fig. 5. Both scales indicate four decades of pressure and can be read easily in each decade of the scale.
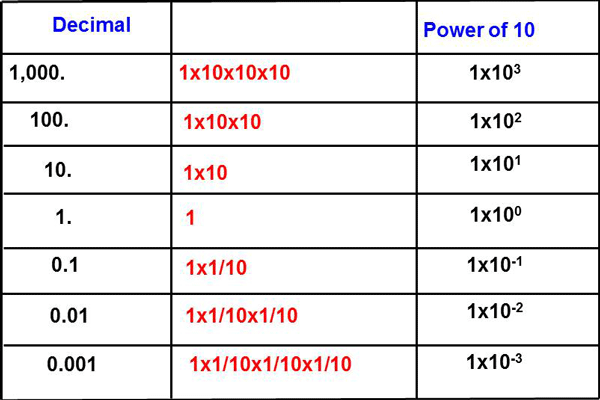
With the change from linear to logarithmic scales, and the increased number of small vacuum measuring units to read, the numbers on the scale were also changed to use scientific notation. This makes the analog scales less cluttered with numbers. Most readers will be familiar with positive scientific notation “powers of ten” where 102 =100 and 103 = 1000 etc. as the square of a number can indicate area and the cube of a number can indicate volume, but negative powers of ten are not always easily understood. Very simply the negative power of ten represents how many places to the left the decimal point has moved as the numbers get smaller from 1.0 every decade. (See Fig.6)
Many modern gauges are now digital rather than analog and these automatically indicate the decade of pressure as well as indicating whatever vacuum measuring unit you select. (See Fig. 7)
Different applications of vacuum in industry and science tend to use a favorite vacuum measuring unit, but from this discussion we can see the relationship between them.
References:
References: Sparnaay, M.J. 1992 Adventures In Vacuums Published by North-Holland, The Netherlands
Technical training material developed by the author.
Copyright Howard Tring, Tring Enterprises LLC Vacuum & Low-Pressure Consulting.
